Greenhouse Gases and Earth’s Energy Balance

Earth’s Energy Balance. 1

1. The Meaning of Temperature and Energy. 1

Temperature. 1

Energy. 2

2. The Temperature of the Early Earth. 2

A. Simple Calculation of Early Earth Temperature. 3

B. More Complicated (but more accurate) Calculation of Early Earth Temperature. 4

3. The Greenhouse Effect and Natural Greenhouse Gases 6

Shortwave Radiation Budget 6

Summary. 8

Global Warming Potential of Greenhouse Gases and the Energy (Im)Balance of Our Current Atmosphere 8

1. Natural Climate Change. 8

2. Radiative Forcing. 12

3. Global Warming Potential 15

Summary 17

Earth’s Energy Balance

1. The Meaning of Temperature and Energy

Temperature

We have discussed temperature in this course without defining what we mean. It's hard to spend a winter in Michigan without having an intuitive feel for temperature, but to understand planetary temperatures and greenhouse warming we need a more precise physical meaning.

All matter (gases, liquids and solids) is made up of atoms in various chemical relationships. Atoms consist of a nucleus orbited by electrons, and are extremely tiny; there are about 10,000,000,000,000 atoms in a cubic centimeter! Because the numbers are so large it usually makes sense to talk about average properties.


	Figure 1. In a hot body, the atoms move rapidly (individual atoms have different speeds, but the mean speed is high). In a cold body, the atoms have relatively low speeds. If collisions occur between hot and cold atoms, the average speed of the atoms (and therefore the temperature) would be intermediate between the high and low cases.

Atoms move randomly, jiggling furiously (at speeds of tens of kilometers per second) and continually colliding with each other. When a cold object (such as a hand) comes into contact with a hot object (say a hot kettle) energy is transferred by these atomic collisions from the hot to the cold body. The energy flows from hot to cold because the atoms in the cold body are pushed to greater speeds (see Figure 1).

Temperature is a measure of the average speed of the moving atoms. The faster they jiggle, the higher the temperature. The mathematical definition tells us that temperature increases as the (mean atomic speed)².

Mathematically we say: , where v is the average atomic speed.

Temperature is measured in units called degrees. For science, the most useful scale is the Kelvin scale. The Kelvin scale starts from a value of absolute zero--a temperature corresponds to perfectly stationary atoms (a situation that cannot be attained in practice). Each degree Kelvin is equivalent to one degree Celsius, with 273K equal to 0^oC). The Earth's mean surface temperature is about 300K.

Energy

There are several types of energy. Some are :

Kinetic energy: energy associated with motion
Potential energy: energy associated with position
Internal energy: energy associated with atomic speed
Radiant energy: energy associated with radiation
Chemical energy: energy associated with chemical bonds

Energy has to be conserved; it can change forms but the total amount must remain the same. We cannot create or destroy energy. This is the famous Conservation of Energy Principle.

2. The Temperature of the Early Earth

Let's calculate the temperature of the early Earth. The initial hydrogen and helium have probably been lost through gravitational escape processes and the atmosphere as we know it today has not yet evolved. We are left with a planet that is cold and airless. We can calculate the temperatures expected for airless planets warmed by the Sun's rays in two ways. First, let's use a radiation law known as the "R-squared" Law.

The R-Squared law states that the farther you are from an emitting object, the less light you receive. In fact, a doubling of the distance away reduces radiation by a factor of four. This is best explained with a picture (see Figure 2).

We expect planets farther from the Sun to be colder. The R-squared model allows us to calculate how much colder each successive planet would be, based on an estimate of the amount of light received. We can use this law to calculate the temperatures of each planet using the current-day temperature of Mercury as a reference.

Figure 2: R-squared law

Figure 2. R-squared Law.

A. Simple Calculation of Early Earth Temperature

Figure 3. The relative rate at which temperature should drop leaving the sun if only accounting for amount of available solar radiation versus relative temperature drop actually observed.

If we assume that Mercury's temperature has not changed, we can calculate the reduction in energy received by each planet using the R-Squared Law, knowing only its mean distance from the Sun.

Figure 3 shows the results of this calculation compared with the actual current day temperatures of the planets. We can see that the simple model does not work very well. Venus is much, much hotter than we would expect. Earth, Mars, Jupiter and Saturn are also hotter than expected - what is going on??

Let's see if we can get a more accurate model of the temperature of Early Earth. This model is slightly more complicated. (You will not be examined on the following).

B. More Complicated (but more accurate) Calculation of Early Earth Temperature.

The principle of Conservation of Energy tells us that the energy from the Sun absorbed by a planet must equal the energy lost by the planet. Since the planet floats in space, the only way to add or subtract energy is through radiation. Therefore we can say for the Earth:

Rate of absorption of energy from the Sun = Rate of emission of radiation to space.

The amount of energy radiated to space from the Early Earth depends on its temperature. Temperature can be calculated using the Stefan-Boltzmann Law. Let's go through the simple arithmetic to calculate the temperature of the Early Earth.

First, recall the types of radiation that the Sun and Earth emit (Figure 4).

Figure 4. Solar and Terrestrial Radiation.

The Sun emits a lot of light in the visible range of wavelengths. We assume that the portion of this light that hits the Earth is absorbed. The Early Earth emits in the infrared. We assume that all of this radiation is lost to space.

The Law of Conservation of Energy tells us that the amount lost (in the infrared) has to equal the amount received (in the visible). Another way of viewing this is to say that the temperature of the Early Earth has to rise until exactly as much energy is lost through radiation as is gained from solar absorption. This equilibrium sets the temperature of any atmosphereless planet.

To calculate the temperature, we need to know how much light is received by the Earth and how much is lost through emission. Let's do this in easy steps.

Step 1.

According to the Stefan-Boltzmann Law, the amount of light emitted by the Sun =,
where T_s is the temperature of the solar surface (assume 6000°K).

Step 2.

The amount of this light that is absorbed by the Earth can be determined if we recognize that the sunlight is "diluted" by the time it reaches the Earth's orbit by a factor of where R_s is the radius of the Sun and r_s is the Earth-Sun distance. This dilution is due to the "R-squared" law discussed above.

Therefore, the light received by the Earth is given by:

where r_e is the radius of the earth. (Energy input = amount emitted by the Sun multiplied by the R-squared dilution factor and by the area cut out of the Sun's radiation beam by the earth) (see Figure 5)

Figure 5. The amount of sunlight falling on the Earth per square centimeter is given by multiplying the intensity at the Earth's orbit by the area cut out of the Sun's radiation beam by the Earth.

Step 3.

We can also write down the amount of radiative energy lost from the Earth, again using the Stefan-Boltzmann law: , where T_e is the temperature of the Early Earth. (Energy output = amount emitted per unit area of the Earth multiplied by the surface area of the Earth)

Step 4.

Using the Law of Conservation of Energy, equate energy input to energy output and solve the equation for T_e:
(Energy input = Energy output)

After cancellation: Te^4=(Rs2/rs2)(Ts^4/4)

Step 5.

Calculate T_e.

For the Early Earth T_e = 283°K.

Step 6.

This calculation assumes that all the sunlight falling on the Early Earth was absorbed. If we assume that some of it (say 83%, like modern day Mars) is reflected, the temperature is 260^oK. This is about 40^o colder than the temperature today - for reasons to be explained below.

We have just calculated the Radiative Equilibrium Temperature of the Earth. It is the temperature that the Earth would have with no atmosphere, when infrared emission exactly balances the radiation received by the Sun.

But, we know that our actual temperature today is ~300°K. What is wrong with our calculation? The atmosphere is responsible for increasing the actual temperature above the radiative equilibrium temperature. This increase is the so-called Greenhouse Effect.

3. The Greenhouse Effect and Natural Greenhouse Gases


	Figure 7: Simple picture of Radiative Transfer (in terms of percentage)

Shortwave Radiation Budget

Results from a more sophisticated calculation than the one described previously demonstrate the magnitude of the natural Greenhouse Effect for the planets (see Figure 6).

The natural greenhouse effect is responsible for life as we know it, and should be distinguished from the infamous anthropogenic greenhouse effect that is currently causing so much concern. The natural Greenhouse Effect is beneficial and warms our planet to more livable temperatures.

Why are the planets warmer than expected on the basis of theory? The answer is that certain gases in the atmospheres of these planets act to warm them up. The explanation is best understood by reference again to the type of radiation emitted by the Sun and by the planets (see Figure 7, below). Note that we need an extra 70% leaving the top to achieve equilibrium. Where does it come from?

Over a long term average, the Earth and its atmosphere must radiate as much energy out to space as it receives from the sun. In fact, the same type of balance exists between the Earth and its atmosphere!

Albedo (L) = percentage of incoming radiation that is reflected back into space = 30% for Earth
(higher for Venus)

Longwave Radiation Budget

Now let's look at the long wave (IR) component of the planetary radiation budget (Figure 8):


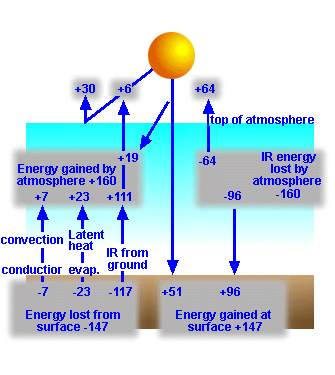
	Figure 8: Infrared component of the planetary radiation budget

At the Earth's surface, we note that the gain and loss in energy is greater than that received from the Sun - how can this be?

Earth's Surface
Gains		Losses
51	Visible from Sun	7	Conduction, Convection
96	IR from atmosphere	23	Evaporation
		117	IR radiation
147	net	147	net

The answer makes sense when we consider that the surface of a planet receives a great deal of energy from its own atmosphere. Thus the effect of the atmosphere is to warm the surface over the temperature above that resulting from the Sun's energy.

We then have to ask, how does the atmosphere increase the Earth's temperature?

The atmosphere warms the Earth by "trapping" radiation, allowing the surface to warm to 300K. At that temperature, the black body surface radiation is large enough to ensure that an equilibrium condition pertains. The atmosphere traps radiation through the action of certain gases, called Greenhouse Gases. These gases (e.g., CO₂, H₂O, NO, CFCs, CO) are very good at absorbing and re-emitting infrared radiation. They intercept the IR radiation from the ground and reflect some of the energy back to the ground, warming it up more than would occur otherwise.

The Greenhouse Effect provides additional heat!

Summary

Temperature is a measure of the square of the mean speed of atoms and molecules.
Energy comes in different types, but must be conserved as a whole.
The temperature of the early Earth (and other airless planets and satellites) was determined by the balance between the absorption of solar visible light and the emission of infra-red light. The temperature that allows these energy sources and sinks to balance is called the radiative equilibrium temperature.
The Greenhouse Effect allows certain planets to warm up above their respective radiative equilibrium temperatures. The effect is due to the presence in the atmosphere of Greenhouse gases, such as CO₂, H₂O, NO, etc.

Global Warming Potential of Greenhouse Gases
and the Energy (Im)Balance of Our Current Atmosphere

Driving Questions:

What's processes lead to temperature change?
What gases comprise the atmosphere and how do they influence the temperature?
What are the global warming potentials for greenhouse gases?

1. Natural Climate Change

We believe that the temperature of the earth has varied wildly over the evolution of the earth. Figure 1 shows an estimate of temperature changes as complied by Scotese. So how can it be that the climate has changed so over the ages and what processes could lead to these changes?

Figure 1. Estimated changes in global temperature

The processes for changing climate naturally include:

Plate tectonics
Volcanic eruptions
Solar Variations, and
Orbital Variations

Plate Tectonics

The movement of the continents has obviously influenced the climate at specific locations (Figure 2), but could also influence the global temperature by redistributing the collection of solar radiation and/or providing land masses on which continental glaciers could form.

Figure 2. Location of continents during the Devonian period from Scotese

Volcanic Eruptions

The amount and location of material added to the atmosphere by volcanoes probably has significantly influenced climate over the ages. Volcanoes emit some greenhouse gases like CO₂ and H₂O, but also emit SO₂ that can get trapped in the upper parts of the atmosphere where it will react to form sulfates, a small particle. These particles can reflect incoming radiation to lower the surface temperature.

Figure 3. NOAA monitors the amount or particles (aerosols) in the atmosphere. Note aerosols over northern and southern Africa. Click here for a current image.

Solar Variability

Variations in sunspot activity result in changes on the order of 0.1% to 0.2 over 11 year cycle. Numerical climate models predict that a change in solar output of only 0.5% per century could alter the Earth's climate.

Figure 4. The changing amount of the solar surface covered by the biggest sunspots,
Earth would be 169 millionths on the chart. (Courtesy Rich J Niciejewski, U. Mich)

Orbital Variability

The Earth's orbit changes over time in ways that could influence the amount of energy received at the surface. These include changes in eccentricity, precession of the equinox, and changes in the Earth's tilt (obliquity).

Eccentricity

The eccentricity of the Earth's orbit changes with a period of 100,000 years. At the moment the Earth's orbit is fairly circular but in 50,000 years it will be more eccentric with the difference between aphelion (farthest) and perihelion (nearest) points in the orbit will become larger.

Precession of the Equinox

Now the Earth is closest the sun in January and farthest in July. The combination of changing eccentricity and precession of the equinox leads to changing available solar radiation.

Obliquity

Finally, the Earth wobbles on its axis of rotation changing the tilt of the Earth (and hence its seasonality) over a 41,000 year period. The tilt is now 23.5¼ but changes between 22.5¼ and 24.5¼.

2. Radiative Forcing

The temperature of the Earth's surface and atmosphere are dictated by a balance between incoming energy and outgoing energy. Temperature rises when more energy is received than lost. The Earth's surface, for example, absorbs radiation from the Sun. This energy is then redistributed by the atmospheric and oceanic circulations and radiated back to space at longer (infrared) wavelengths. For the annual mean and for the Earth as a whole, the incoming solar radiation energy is balanced approximately by the outgoing terrestrial radiation. Any factor that alters the radiation received from the Sun or lost to space, or that alters the redistribution of energy within the atmosphere and between the atmosphere, land, and ocean, can affect climate. A change in the net radiative energy available to the global Earth-atmosphere system is termed a radiative forcing. Positive radiative forcing tends to warm the Earth’s surface and lower atmosphere. Negative radiative forcing tends to cool them.

Increases in the concentrations of greenhouse gases will reduce the efficiency with which the Earth’s surface radiates to space. More of the outgoing terrestrial radiation from the surface is absorbed by the atmosphere and re-emitted at higher altitudes and lower temperatures. This results in a positive radiative forcing that tends to warm the lower atmosphere and surface. Because less heat escapes to space, this is the enhanced greenhouse effect – an enhancement of an effect that has operated in the Earth’s atmosphere for billions of years due to the presence of naturally occurring greenhouse gases: water vapor, carbon dioxide, ozone, methane and nitrous oxide. The amount of radiative forcing depends on the size of the increase in concentration of each greenhouse gas, the radiative properties of the gases involved (indicated by their global warming potential), and the concentrations of other greenhouse gases already present in the atmosphere. Further, many greenhouse gases reside in the atmosphere for centuries after being emitted, thereby introducing a long-term commitment to positive radiative forcing.

Anthropogenic aerosols (microscopic airborne particles or droplets) in the troposphere, such as those derived from fossil fuel and biomass burning can reflect solar radiation, which leads to a cooling tendency in the climate system. Because it can absorb solar radiation, black carbon (soot) aerosol tends to warm the climate system. In addition, changes in aerosol concentrations can alter cloud amount and cloud reflectivity through their effect on cloud properties and lifetimes. In most cases, tropospheric aerosols tend to produce a negative radiative forcing and a cooler climate. They have a much shorter lifetime (days to weeks) than most greenhouse gases (decades to centuries), and, as a result, their concentrations respond much more quickly to changes in emissions. Volcanic activity can inject large amounts of sulfur-containing gases (primarily sulfur dioxide) into the stratosphere, which are transformed into sulfate aerosols. Individual eruptions can produce a large, but transitory, negative radiative forcing, tending to cool the Earth’s surface and lower atmosphere over periods of a few years.

When radiative forcing changes, the climate system responds on various time-scales. The longest of these are due to the large heat capacity of the Deep Ocean and dynamic adjustment of the ice sheets. This means that the transient response to a change (either positive or negative) may last for thousands of years. Any changes in the radiative balance of the Earth, including those due to an increase in greenhouse gases or in aerosols, will alter the global hydrological cycle and atmospheric and oceanic circulation, thereby affecting weather patterns and regional temperatures and precipitation.

Solar radiation budget

Figure 5. Global average flow of shortwave (solar) radiation through the Earth's atmosphere